Cesestial Navigation Computer Programs
Find your actual position by direct computation
without plotting on a chart
written by J. R. Mathison
March 2016
GO TO Home Page
for more technical articles.
- Links to individual sections below
- GO TO PAGE OVERVIEW
- GO TO PROGRAM DESCRIPTIONS
- GO TO PROGRAM ACURACY
- GO TO AN EXAMPLE USING 'ICE'
- GO TO MOVING A LINE OF POSITION
- GO TO HOW TO GET
LATITUDE AND LONGITUCE FROM A ROAD MAP
- GO TO MISCELANEOUS
- GO TO DOWNLOAD PROGRAMS
PAGE OVERVIEW
This page details the use of three computer programs written as
an aid to finding your actual geographic position when using
celestial navigation.
This is NOT a tutorial. I assume that you already know how to
use celestial navigation. If not, there are lots of tutorials to
be found on the internet.
If you do NOT know anything about celestial navigation, a very
brief description follows:
You need to know the date and time of day. A watch can be set to
good acuracy using the shortwave radio signals from WWV at Ft.
Collins, Colorado.
You need a sextant to measure the altitude of a heavenly body,
and you need a 'Nautical Almanac' to get the 'geographical
position' (GP) on earth of that heavenly body.
Select a heavenly body and measure it's altitude with the
sextant. Look up that heavenly body in the 'Nautical Almanac' to
find it's 'geographical position' (GP) on earth. You will be
somewhere on a 'circle of equal altitude' centered around that
GP, and with a radius of 90 degrees minus the corrected sextant
altitude. (90 - Hc = co-altitude).
See drawing below at left.
Select a second heavenly body and measure it's altitude and find
it's GP. You will also be somewhere on another 'circle of equal
altitude' centered around the second GP.
In the drawing below at left, note that two circles intersect in
two points. You will be on ONE of them.
Select a third heavenly body, and it's 'circle of equal altitude'
will intersect with the first two circles with only ONE point in
commom, your actual location.
The whole 'circle of equal altitude' or 'line of position' is
much too large to plot onto a map or chart of a smaller area.
The traditional method uses a small part of the circle near an
'Estimated Position' (EP) to plot onto a map. This small part of
the circle can be represented by a short straigh line. An
altitude is measured to a heavenly body from your 'actual
position' (AP), and the difference is noted between that measured
altitude and what the 'corrected sextant altitude' (Hc) for the
(EP) from the Nautical Almanac. A short line is plotted onto the
map at a right angle to the azmuth to the heavenly body, and at
an arc distance toward or away from the (EP) by the above
difference. Repeat the process of this paragraph for a second
heavenly body, and where the two short lines cross is your (AP).
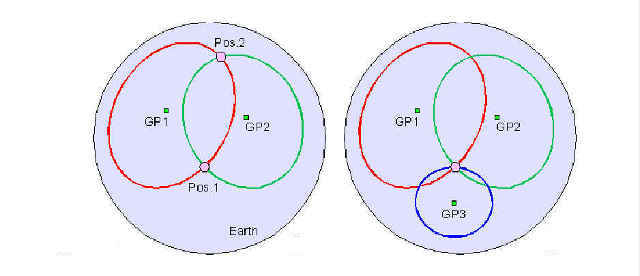The two drawings to the right show that 'lines of position' from
a geographical position (GP) are circles. The circle is the
locus of all points on earth where the altitude is exactly the
same to a given heavenly body. Your actual position is somewhere
on that circle. You can narrow that down to two possible
locations by getting the altitude to a second heavenly body, and
you can get your actual position by getting the altitude to a
third heavenly body.
My computer program 'cel_nav-position' calculates your position
without the need to plot anything on a map or chart.
PROGRAM DESCRIPTIONS
Program 'cel_nav-position' for linux or 'C-N-POS.EXE' for DOS
outputs the two geographical positions of the two intersections
of the two circles which are the respective 'lines of position'
from any two geographical positions of heavenly bodies or from
any two known geographic positions on a map.
The program requires entry of the two geographical positions of
the heavenly bodies and their respective sextant co-altitudes
(90 - Hc). Output is the two positions of the intersection of
the two 'circles of equal altitude'. See Pos1 and Pos2 in the
drawing above. Output also goes to logfile 'position.txt'
.
Program 'cel_nav-run_lop' for linux or 'C-N-LOP.EXE' for DOS
outputs a second geographical position by moving from the first
geographical position along a given bearing and for a great
circle arc distance.
The program requires entry of a geographical position, a bearing,
and an arc distance. Output is the new geographical position,
the bearing to and from new and old geographical positions, and
the arc distance between them. Output is also to logfile
'run-lop.txt'.
.
Program 'cel_nav-distance' for linux or 'C-N-DIST.EXE' for DOS
outputs the great circle arc distance and bearings to and from
two geographical positions.
The program requires entry of two geographical positions. Output
is the two geographical positions, bearing to and from each, and
the arc distance between them. Output also goes to logfile
'distance.txt'.
.
You will also need a table of ephemeris of the heavenly bodies
which can be used in celestial navigation. I use 'The U.S. Naval
Observatory Nautical Almanac', Floppy Version 2.00.88, also know as
'ICE' which is now in the public domain. An internet search will
find where to download it. Users of UNIX or Linux will need a DOS
emulator, such as 'dosbox' to run this program. Also, users of
UNIX or Linux will probably need to recomplie my UNIX or Linux
versions to run on your operating system. The source code '*.c'
is included for your re-compilation. Probably all you need to do
is run at the command prompt:
gcc cel_nav-position.c -lm -o cel_nav-position.xxx
gcc cel_nav-run_lop.c -lm -o cel_nav-run_lop.xxx
gcc cel_nav-distance.c -lm -o cel_nav-distance.xxx
I always append the '.xxx' to identify an executable file.
If you do not want to re-compile, run the DOS versions under
'dosbox' or another DOS emulator.
Microsoft users will find that the DOS versions of my programs
and 'ICE' run just fine in a 'command prompt' or 'DOS prompt'
window.
DISCLAIMER
My background is in avaition and I have never used celestial
navigation. I wrote these programs as an AID to celestial
navigation and you should test them thoroughly against proven
methods before relying on them.
I assume that someone else has already written programs to find
your actual position on earth without plotting on a map or chart.
My internet searches did not find anything in the public domain.
PROGRAM ACURACY
An example of the accuracy of program 'cel_nav-position' follows.
AP = Actual Geographic Position of observer
GP = Geographic Position of a heavenly body
Our actual position is at 45 degrees N. latitude, and 107 degrees W. longitude.
GP1, GP2, and GP3 are the fictious geographical positions of three heavenly
bodies obtained by running 'cel_nav-run_lop' three times.
First entering 45 deg N. lat, 107 W. long, bearing 10 degrees,
and 80.000000 arc degrees.
Second entering 45 deg N. lat, 107 W. long, bearing 130 degrees,
and 75.000000 arc degrees.
Third entering 45 deg N. lat, 107 W. long, bearing 250 degrees,
and 70.000000 arc degrees.
Hc is the corrected sextant altitude.
GP1 latitude: 53.956714 and longitude: -56.103869,
Hc = 10.000000 degrees, so co-altitude = 80.000000 arc degrees
GP2 latitude: -14.833998 and longitude: 57.052653,
Hc = 15.000000 degrees, so co-altitude = 75.000000 arc degrees
GP3 latitude: 0.835690 and longitude: 169.020579,
Hc = 20.000000 degrees, so co-altitude = 70.000000 arc degrees
GP1 and GP2 entered into program 'cel_nav-position' to calculate
the intersection of the two circles (lines of position):
:) Position 1-?? co-ords are latitude: 45.000000 and longitude 106.999999
and in DMS format latitude: 45 0 0 and longitude 106 59 59
:) Position 2-?? co-ords are latitude: -20.533270 and longitude: -22.186549
and in DMS format latitude: -20 31 59 and longitude: -22 11 11
GP2 and GP3 entered into program 'cel_nav-position' to calculate
the intersection of the two circles (lines of position):
:) Position 1-?? co-ords are latitude: 45.000000 and longitude 107.000000
and in DMS format latitude: 44 59 59 and longitude 106 59 59
:) Position 2-?? co-ords are latitude: -66.805905 and longitude: 143.515002
and in DMS format latitude: -66 48 21 and longitude: 143 30 54
GP1 and GP3 entered into program 'cel_nav-position':
:) Position 1-?? co-ords are latitude: 45.000001 and longitude 107.000000
and in DMS format latitude: 45 0 0 and longitude 107 0 0
:) Position 2-?? co-ords are latitude: -5.219815 and longitude: -121.149833
and in DMS format latitude: -5 13 11 and longitude: -121 8 59
:) Position 1-?? co-ords are latitude: 45.000000 and longitude 107.000000
in all three cases above, plus or minus 0.000001 degree (0.3648
feet), which was our actual geographical position (AP) at the
begining of this test. These programs are highly acurate!
AN EXAMPLE USING 'ICE'
Note: 'ICE' requires that west longitudes be negative and
east longitudes be positive.
Celestial Navigation Data for 2016 Mar 13 at 5 00 00 UT (GMT)
For Assumed Location: Longitude W 107 00.0, Latitude N 45 00.0
The three stars were selected below based on their approximate
120 degrees in azmuth from each other for highest accuracy.
Note: GHA (Greenwich Hour Angle) above 180 degrees longitude
must have 360 degrees subtracted to get negative east longitudes
used in 'cel_nav-position'
Note: (ICE) 'Interactive Computer Ephemeris' requires that East
Longitudes be positive and West Longitudes be negative.
North Latitudes are positive and South Latitudes are negative.
(GHA) Greenwich Hour Angle is longitude. If (GHA) is over 180
degrees, subtract 360 degrees from it to get negative East
Longitudes to enter into 'cel_nav-position'.
(Dec) declination is latitude. Hc is corected sextant altitude.
The line directly below 'SUN' below is my converting of minutes
to decimal parts of a degree. 90 - Hc = co-alt
Object GHA Dec Hc Zn
ALPHECCA 12 25.0 n26 39.5 +15 28.3 67.6
12.416667 26.658333 (90 - 15.471667) = 74.528333 co-lat
Enter into 'cel_nav-position':
26.658333 N. lat, 12.416667 W. lon, and 74.528333 co-lat
PROCYON 131 13.4 n 5 10.7 +44 54.8 215.2
131.223333 5.178333 (90 - 44.913333) = 45.086667 co-lat
Enter into 'cel_nav-position':
5.178333 N. lat, 131.223333 W. lon, 45.086667 co-lat
SCHEDAR 235 54.6 n56 37.5 +20 15.2 332.9
235.910000 56.6250 (90 - 20.253333) = 69.746667 co-lat
-124.090
Enter into 'cel_nav-position':
56.6250 N. lat, -124.090 E. lon, 69.746667 co-lat
Entering ALPHECCA and PROCYON into 'cel_nav-position':
:) Position 1-?? co-ords are latitude: 44.999922 and longitude 106.999731
and in DMS format latitude: 44 59 59 and longitude 106 59 59
:) Position 2-?? co-ords are latitude: 2.101546 and longitude: 86.140309
and in DMS format latitude: 2 6 5 and longitude: 86 8 25
Entering PROCYON and SCHEDAR into 'cel_nav-position':
:) Position 1-?? co-ords are latitude: 45.000028 and longitude 106.999943
and in DMS format latitude: 45 0 0 and longitude 106 59 59
:) Position 2-?? co-ords are latitude: 4.621591 and longitude: 176.481265
and in DMS format latitude: 4 37 17 and longitude: 176 28 52
Entering SCHEDAR and ALPHECCA into 'cel_nav-position':
:) Position 1-?? co-ords are latitude: 45.000073 and longitude 106.999819
and in DMS format latitude: 45 0 0 and longitude 106 59 59
:) Position 2-?? co-ords are latitude: 5.570607 and longitude: -63.049987
and in DMS format latitude: 5 34 14 and longitude: -63 2 59
Note again that:
:) Position 1-?? co-ords are latitude: 45.000000 and longitude 107.000000
in all three cases above, plus or minus one second (101.3 feet).
This was our actual geographical position at the begining of this test.
The above is another testament to the acuracy of the computations
and the acuracy of the 'ICE' program for using stars to find
your actual position. Using the sun is not quite as acurate as
noted farther below.
MOVING A LINE OF POSITION
Sun run Sun method.
Using 'cel_nav-run_lop' to move a 'line of position' (LOP).
Island Hopping on the high seas.
Leaving Palmyra Atoll and headed towards Johnston Atoll at 15
kts. aboard a yacht.
Palmyra Atoll: 5 53' N., 162 5' W. UTC = Local time + 11 hours
5.883333 162.083333
Johnston Atoll: 16 45' N., 169 31' W. UTC = Local time + 11 hours
16.750 169.516667 AND the distance apart:
Run 'cel_nav-distance', input: 16.750, 169.516667, 5.883333, 162.083333 and:
Location A: 16.750000, 169.516667 (Johnston Atoll)
Location B: 5.883333, 162.083333 (Palmyra Atoll)
The distance A to B is 0.228251 rad or 13.077835 arc deg
The bearing from B to A is 5.703821 rad or 326.804896 deg
The bearing from A to B is 2.536621 rad or 145.337681 deg
Note above: The starting bearing is 326.804896 deg and the ending
bearing is 145.337681 + 180 = 325.337681 degrees. There is a
course correction of 1.467 degrees over the 784.6701 nm route.
13.077835 x 60 = 784.6701 nm, @ 15 kts = 52.31 hours
GP = Geographic Position of a heavenly body
EP = Estimated Position of observer
Leaving Palmyra Atoll Monday Dec 1, 2014 at 9am local time, 2000 UTC,
at 15 kts, and steering for a course with a bearing of 326.804896 degrees
towards Johnston Atoll.
At Tuesday, Dec 2, 2014 at 9am local time, 2000 UTC, we should have gone
360 nm or an arc distance of 6.000 degrees from start.
We should be at EP 1: latitude: 10.891601 N. and longitude: 165.424325 W
At Tuesday, Dec 2, 2014 at 3pm local time, (2600 UTC)
which is Wednesday Dec 3, 2014, (0200 UTC) we should have gone 450 nm
or an arc distance of 7.5 degrees from start.
We should be at EP 2: 12.138567 N., 166.275181 W.
The distance from EP1 to EP2 is:
Run 'cel_nav-distance' 10.891601, 165.424325, 12.138567, 166.275181
Location A: 12.138567, 166.275181 (EP2)
Location B: 10.891601, 165.424325 (EP1)
The distance A to B is 0.026180 rad or 1.500000 arc deg
The bearing from B to A is 5.695305 rad or 326.316962 deg
The bearing from A to B is 2.550748 rad or 146.147096 deg
The sun sight (the sun's GP) taken at EP1 must be moved forward
1.500000 arc degrees at a bearing of 326.316962 degrees.
DATA FROM 'ICE':
Note: (ICE) 'Interactive Computer Ephemeris' requires that East
Longitudes be positive and West Longitudes be negative.
North Latitudes are positive and South Latitudes are negative.
(GHA) Greenwich Hour Angle is longitude. If (GHA) is over 180
degrees, subtract 360 degrees from it to get negative East
Longitudes to enter into 'cel_nav-position'.
(Dec) declination is latitude. Hc is corected sextant altitude.
The line directly below 'SUN' below is my converting of minutes
to decimal parts of a degree. 90 - Hc = co-alt
TAKE SUN SIGHT ONE (GP1) AT EP1:
Celestial Navigation Data for 2014 Dec 2 at 20 00 00 UT (GMT)
Delta T = 77.9 seconds
For Assumed Location: Longitude W 165 25.4
Latitude N 10 53.5
Almanac Data
Corrections
Object GHA Dec Hc Zn
SUN 122 37.4 s22 01.6 +36 39.6 128.3
122.623333 -22.026667 (90 - 36.660 = 53.340 co-alt)
The sun sight (the sun's GP) taken at EP1 must be moved forward
1.500000 arc degrees at a bearing of 326.316962 degrees:
Enter into 'cel_nav-run_lop':
-22.026667, 122.623333, 326.316962, 1.5 and
New GP1: latitude: -20.776111 and longitude: 123.513022
and 53.340 co-alt
TAKE SUN SIGHT TWO (GP2) AT EP2:
Celestial Navigation Data for 2014 Dec 3 at 2 00 00 UT (GMT)
Delta T = 78.0 seconds
For Assumed Location: Longitude W 166 16.5
Latitude N 12 08.3
Almanac Data
Corrections
Object GHA Dec Hc Zn
SUN 212 35.9 s22 03.7 +33 08.6 233.2
212.598333 -22.061667 (90 - 33.143333 = 56.856667 co-alt)
-147.401667
Enter into 'cel_nav-position':
-20.776111, 123.513022, 53.340 and
-22.061667, -147.401667, 56.856667
which yields:
:) Position 1-?? co-ords are latitude: 12.105076 and longitude 166.249609
and in DMS format latitude: 12 6 18 and longitude 166 14 58
:) Position 2-?? co-ords are latitude: -69.507022 and longitude: 159.518099
and in DMS format latitude: -69 30 25 and longitude: 159 31 5
Note: :) Position 1 above is quite close.
EP 2: 12.138567 N., 166.275181 W. (from dead reckoning)
- 12.105076 - 166.249609 (from 'cel_nav-position')
= .033491 = .025572 (range in degrees of arc)
2.01 nm in lat, 1.5 nm in lon at equator (range in nm)
Note: Since this is another hypothetical example, (EP) is not
'estimated position' it is (AP) = 'actual position'.
HOW TO GET LATITUDE AND LONGITUCE FROM A ROAD MAP
I wanted to look at air photos in the area of an early day
homestead in Northwestern South Dakota where the present day road
from Mud Butte to Prairie City crosses the South Fork of the
Moreau River, and I needed the geographic co-ordinates to plug into
a search engine.
An internet search gives the GP of three nearby small towns to
enter into program 'cel_nav-position':
Redig: 45.27111 N., 103.54778 W., 34 sm to place of interest
Bison: 45.52389 N., 102.46472 W., 37 sm to place of interest
Fairpoint: 44.74833 N., 102.79667 W., 25 sm to place of interest
The statute miles (sm) above must be converted to arc degrees to
put into program 'cel_nav-position' by multiplying the sm by
0.0144737, and the above becomes:
Redig: 45.27111 N., 103.54778 W., 0.4921 degrees of arc
Bison: 45.52389 N., 102.46472 W., 0.5355 degrees of arc
Fairpoint: 44.74833 N., 102.79667 W., 0.3618 degrees of arc
After entering the above in pairs three times, the output of
'cel_nav-position' is:
:) Position 1-?? co-ords are latitude: 45.694496 and longitude 103.190329
and in DMS format latitude: 45 41 40 and longitude 103 11 25
X . :) Position 2-?? co-ords are latitude: 45.085276 and longitude: 102.901513
and in DMS format latitude: 45 5 6 and longitude: 102 54 5
X . :) Position 1-?? co-ords are latitude: 45.098216 and longitude 102.926721
and in DMS format latitude: 45 5 53 and longitude 102 55 36
:) Position 2-?? co-ords are latitude: 44.989484 and longitude: 102.416110
and in DMS format latitude: 44 59 22 and longitude: 102 24 57
X . :) Position 1-?? co-ords are latitude: 45.103878 and longitude 102.891259
and in DMS format latitude: 45 6 13 and longitude 102 53 28
:) Position 2-?? co-ords are latitude: 44.811721 and longitude: 103.298496
and in DMS format latitude: 44 48 42 and longitude: 103 17 54
'X'. above marks the lines of closest match on the three outputs.
The range of latitudes is 0.018062 degrees or 1.2 sm
and the range of longitudes is 0.035462 degrees or 1.73 sm at 45
degrees of latitude. Average the latitudes and longitudes for
highest accuracy.
MISCELLANEOUS
Hint: Do you need to acurately plot your position on a map? Use
'cel_nav-distance' to get the arc distance from your position to
two published locations on the map and then use your drawing
compass to measure from there and make two intersecting pencil
arcs to pinpoint your location.
Do not enter into program 'cel_nav-position' two geographical
positions which are 180 degrees apart from your position. Doing
so results in two 'circles of equal altitude' which are only
tangent to each other. Since the circles do not overlap, there
is no two points of intersection and the program will fail. The
dos version crashes and the linux version outputs nonsense.
Do not enter into program 'cel_nav-position' or program
'cel_nav-distance' two geographical positions which are on the
same meridan. These programs depend on the polar spherical
triangle, including an angle at the north pole. If this angle is
'zero', there is no polar spherical triangle and these programs
will fail.
You can kill these programs by entering 'CTRL-C' (^c) if you need
to halt their execution.
I would have published these programs years ago but I could not
figure out how to automatically select a 'western' geographical
position and an 'eastern' geographical position depending on
their respective longitudes. The spherical triangle depends on
identifying these positions correctly.
My earlier attempts resulted in failure to measure across the
'international date line' when measuring across the 'greenwich
meridan' worked properly. When I got no errors across the
'international date line', then measurement across the 'greenwich
meridan' would fail. I am happy to say that I finally got it
right.
I am just an amateur programmer in the 'C' language. The source
code (*.c) is included with these programs for your scrutiny.
Those of you who are knowledgeable programmers will probably see
many ways to code these programs for better efficiency.
DOWNLOAD PROGRAMS
The file 'cel-nav.zip' below opens into directory 'cel-nav' with
subdirectories 'dos' and 'linux' containing the dos and linux
versions of the above computer programs.
Download
'cel-nav.zip' here.
.
-
- Please send E-Mail to: mathison (aatt) sdf-eu.org
- .
- Last revision 2016-03-21